量子力学（科普部分）

量子力学随着各种乱七八糟科普书的推广，在大众心中一直以一种奇怪的形象出现。但愿这一篇能更正一部分人乱七八糟的想象。这次会与以往不同，会分为历史、科普、正式三部分。对于物理竞赛的同学来讲，需要的可以自取所需。

一、历史

量子力学的开端，来源于20世纪初“两朵乌云”其中的一朵：黑体辐射的问题。所谓黑体，是黑色的物体……其实是理想中不能反射与透射电磁波、与环境达到热平衡的物体。当然，理想的模型往往是不存在的，然而，一个只留有一个小孔的空腔和黑体已经非常接近了。黑体虽然不能反射电磁波，但它自己依然可以发出电磁波。当黑体达到热平衡时，它吸收的电磁波和发射的电磁波应当是平衡的，使得它的能量不再变化，这时候，它辐射的电磁波称为黑体辐射。如果我们去测量黑体辐射的谱，看看不同频率的电磁波强度分别是多少，会得到一个黑体辐射谱，这个谱的形状只与黑体的温度有关。

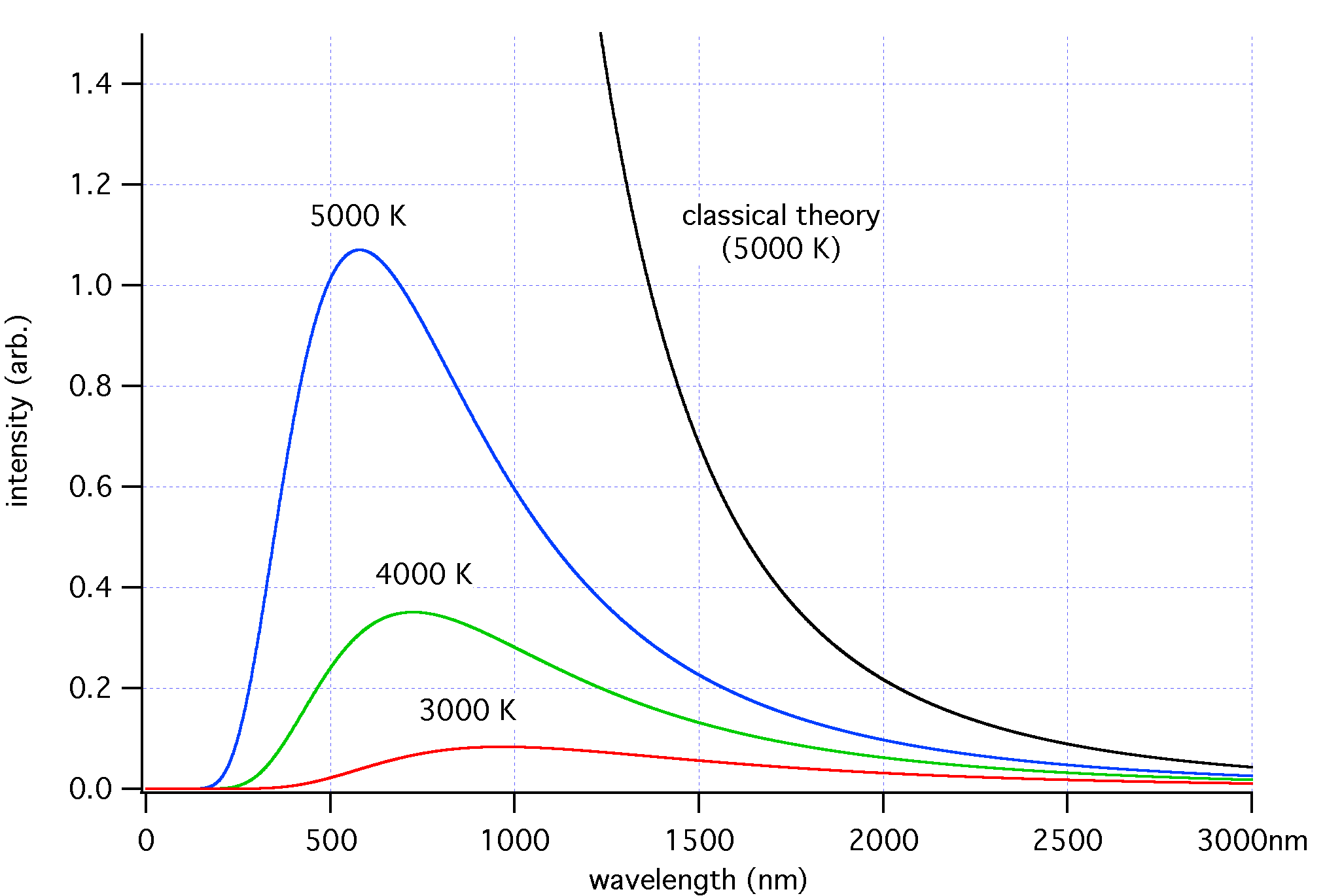（图片取自Wiki）

于是一个自然的想法是用统计力学的方法来解释黑体辐射谱为什么是这个形状。于是，有了Wien近似和Rayleigh-Jeans公式，但这两个曲线的形状都不能完美地吻合实验，一个仅在长波区域符合，另一个仅在短波区域符合。1900年，Planck在改进Wien近似的过程中，唯象地找到了一个公式，能够与实验完美符合，但在解释这个公式的物理意义时，却遇到了麻烦：Planck的公式中电磁场的能量似乎是一份一份而不连续的。然而，作为古典的物理学家，Planck是不会承认这一点的。

1905年，Einstein针对光电效应（这个应该在高中课本中被讨论烂了）提出了光量子的概念，认为电磁波的能量不是连续的，而是以光量子为单位的一份一份的，简称光子。一个光子的能量与光子的频率成正比，而光照的强度只与光子的数目有关。

另一方面，1909年Rutherford发现原子核的存在之后，原子模型也引起了人们的兴趣。因为按照经典的电磁理论，具有加速度的电子会不断辐射电磁波而损失能量，因此原子的行星模型不可能稳定存在。而对原子光谱的测量结果也令人费解，一种原子似乎只能吸收或发射特定频率的光，如果原子的能量是可以连续变化的，应该可以发出任意频率的光才对。为此，1913年波尔提出Bohr模型来解决原子光谱的问题。Bohr模型认为原子核外电子的轨道不是任意的，电子只能在满足特定量子化条件的轨道上运动。这个模型比较好地预测了类氢原子的光谱，但是不能预测其他原子的光谱。

1924年，de Broglie通过类比，提出了物质波的假说，认为电子之类的粒子也具有和光子类似的波动特性。结果，1927年完全与之独立的一个实验组在晶体中观测到了电子的衍射图样，发现电子运动确乎具有波的特征，让de Broglie撞上了大运。

1921年，测量原子磁矩的Stern-Gerlach实验也发现了令人奇怪的结果。实验用一个非均匀的磁场来偏转带有磁矩的银原子，原子带有的磁矩角度与原子被偏转的角度相关。原本人们预期会看到一个宽阔的斑——因为随机运动的原子磁矩应该可以有各种取向，然而实验结果看到的却是两个条带，这意味着原子磁矩只有两个取向，角动量也是量子化的。

1924年为进一步解决原子光谱的问题，泡利提出电子具有一个内禀的双值的自由度，1925年Ralph Kronig、George Uhlenbeck与Samuel Goudsmit提出基本粒子的自转与角动量的概念，1927年泡利提出了形式化的自旋理论。然而电子自旋仍然是一个奇怪的东西，因为电子为达到自旋角动量，其“转动”会超过光速。在量子力学的范畴中，自旋只是被唯象地描述。1928年Dirac提出相对论性的Dirac方程，描述了相对论性电子的运动，而此时电子自然地带有一个内禀的角动量，与自转无关。

关于量子力学的公理形式，1920年代先后有Schrödinger的波动力学与Heisenberg的矩阵力学，后来1926年Schrödinger证明了两种力学的等价性，于是（非相对论性）量子力学的公理形式便完成了。1948年，Feynman提出路径积分表述，作为第三种构建量子力学的方式，并明确了量子力学与经典力学的关系。其思想可以参见理论力学——哈密顿力学 – Everything is Physics 万物皆理 – 知乎专栏最后一节。

至此提出的量子力学是不包含相对论的。关于相对论性量子力学有诸多尝试，Schrödinger在提出非相对论性的Schrödinger方程之前，也曾想到了Klein–Gordon方程，但它不能保证粒子出现的概率是正的，具有严重问题。1928年Dirac方程解决了这个问题，但依然有问题：相对论意味着描述单粒子的理论框架不再准确。正式的相对论性的量子理论框架则是1950年代逐渐建立起的量子场论。

二、科普

先推荐一本比较靠谱的量子力学的科普书：

《新量子世界》安东尼·帕特里克·沃尔特斯【摘要书评试读】图书，译者是我的C++老师，北京大学物理学院做核物理的老师。这本书态度诚恳，内容也很准确，准确到几乎感觉就是将普物级别的量子物理书中的公式去掉而已。原则问题绝不含糊，不过缺点是进入场论之后，后半部分展开很难跟上，我当时就没怎么看懂。

微观粒子毁三观的运动方式令人不得不放弃宏观的图像：粒子运动不再具有确定的轨迹，甚至不再具有确定的位置。人们转而描述粒子的状态。关于粒子的状态，最重要的假设是它是可以叠加的。态的叠加特性，按照Sakurai的说法，可以在测量粒子自旋的Stern-Gerlach实验这个“最简单且最量子的”实验中得到验证。一束自旋朝向+z轴的电子，在测量其x方向的自旋时，会观察到具有+x轴方向与-x轴方向自旋的电子各占50%。然而在继续测量这些电子在z方向的自旋时，会发现有一半的电子的自旋变成了-z轴方向。然而，一束自旋朝向+z轴的电子，无论多少次测量其z方向的自旋，都找不到自旋朝向-z方向的电子。

首先，这意味着自旋朝向正z方向的电子并不是两种电子的混合。电子并不是某种贴着“自选方向：+x,+z”与“自选方向：-x,+z”标签的东西。自旋的z方向和x方向存在某种联系，而这种联系最适合用线性代数来描述：一个自旋+z方向的电子状态，是自旋+x方向与-x方向两种状态的叠加。这种叠加，甚至不同于将50%的+x方向与50%的-x方向的两种粒子混合起来。

而两个测量过程不可交换，意味着测量改变了粒子的状态。在经过x方向的自旋测量之后，粒子便不再处于自旋+z方向的状态了。这正是不确定性原理，粒子的某些特征是不能被同时测量的，一旦进行了一个特征的测量，另一个特征就被改变了。比粒子自旋/角动量各个方向的不确定性更有名的，是粒子的位置-动量满足的不确定性原理。实际上，是同样的缘故。

注意时间和能量并没有相应的不确定性原理。在非相对论性的理论中，时间不是粒子的可观测量，不是粒子的属性，只是一个参数。因此，没有与位置-动量类似的不确定性关系，实验上也不存在。相对论性理论中，位置与时间必须要统一处理，因此在场论中，位置也不再是算符，和时间一样变作参数。

然而测量为何会改变粒子的状态，这应该是比较显然的。观察粒子的运动，我们只能通过它和其他东西的相互作用的结果来观察，而这种相互作用，常常会干扰粒子的运动。比如观察粒子的位置，我们要用光子去撞击它，或者让它撞上某个屏幕，这时候，它的动量必然就改变了。在SG实验中，我们用了一个非均匀的磁场干扰了粒子的自旋。注意这里并没有人意识的作用。

测量的结果，就是一个有意思的事情了。测量改变粒子的状态并不是完全随机的，而是只能将粒子的状态改变至特定的几个状态：比如测量x方向自旋之后，你只能得到自旋处于+x方向的粒子和-x方向的粒子，而得不到其他的自旋状态，比如+z，+y等等。然而，我们无法预测会得到具体的哪一个状态，只能预测得到某个状态的概率。

这个过程中究竟发生了什么，历史上有诸多种解释方法，这称为诠释。查看Interpretations of quantum mechanics可以找到现在被提出的所有诠释。但依然需要提醒的是，除了极个别诠释，大多数诠释无法带来可观测的差异，无法在实验中加以区分，因此诠释问题往往并不真正被人关心。下面挑几个比较有名的诠释：
1、隐参量诠释。早期Bohm等人认为微观粒子运动之所以具有不确定性，是因为粒子仍然具有没有被人发现的隐参量，因而造成与统计力学类似的不确定性。这个诠释最接近经典力学的世界观，然而，随着Bell不等式的相关实验，人们发现局域的隐变量是不存在的，因此这个诠释不再被人提及了。

2、多世界诠释。这个诠释被各种科幻小说改编，但基本都是错的。多世界诠释认为波函数被测量时并没有坍缩，只是将观测者与系统纠缠起来，整个宇宙波函数的演化依然是可逆且确定的。观测的不同结果是因为宇宙发生了“分裂”。很多人不喜欢这个诠释，因为它引入了太多不可观测的假设的宇宙。一些更为高级的多世界理论称可以提供可观测的验证，这些我就不清楚了。

3、系综诠释。Einstein等人主张这一诠释。这个诠释认为波函数不是描述单粒子行为的，而是一个描述一堆相近系统的系综。量子力学的结论只是统计意义下的结论，不能用于预测单个粒子的行为。

4、Copenhagen诠释。这个诠释是流传最为广泛影响最大的诠释，很多教材实际上都采用了这一诠释。Copenhagen诠释认为，波函数描述了粒子的全部状态，而这种状态确实是非确定的，测量导致坍缩也确实是存在的。至于为何导致坍缩，Copenhagen诠释并没有提出假说。这种诠释造成了很大的争论，也因此带来了很多佯谬，比如著名的Schrödinger的猫和EPR佯谬。

Schrödinger的猫是这样一个系统：将一只猫置于一个黑盒子中，盒子配备一块放射性物质与盖革计数器，放射性物质在固定时间内有1/2的概率发生衰变，一旦盖革计数器探测到原子衰变，就打破装有氰化物的瓶子将猫毒死。Schrödinger认为，在这系统中，一定时间后猫的状态成为死与活的叠加态，只有人打开盖子时这个量子态才坍缩。猫的生死似乎决定于人打开盖子的行为，这是一个很荒谬的事情。
毕竟Schrödinger的猫是一个佯谬。实际上，宏观的量子纠缠态是存在的，这在一些介观的实验中被观测到了。超导、超流等现象都与宏观的量子纠缠态有关。而另一方面，退相干使得Schrödinger的猫无法稳定在一个确定的纠缠态之中。因为猫、盖革计数器等等都是包含大量粒子的、自由度极高的经典系统，我们几乎无法使它处于确定的量子态之中，与它们发生纠缠的系统会很快脱散。因此，Schrödinger的猫难以长时间维持在叠加态之中。而EPR佯谬也与纠缠态有关。如果我们让两个电子进入总自旋为0的纠缠态，并将两个电子隔离，一旦我们对其中一个电子A进行测量，它的自旋状态会被确定，而由于两个电子总自旋为0，另一个电子B的状态也会被随之确定。Einstein当年认为这其中存在超光速传递信息。在哥本哈根诠释中，另一个电子B波函数的坍缩原因显得有些诡异，似乎测量电子A后有种超光速的信号告诉了电子B，使它的波函数坍缩了。

但是抛开哥本哈根诠释，在观测上，纠缠态其实没有传递任何信息。因为我们无法控制电子A的测量结果。当我们对电子B进行测量后，如果不与保管电子A的那些人联络，我们甚至无从得知电子A有没有被测量。不论A是否被测量，B的测量结果都会是一半自旋向上一半自旋向下。虽然我们测量A之后便立刻知道了B的测量结果，但这种关联，并不是超光速的信息传递。这种“信息传递”的方式就好比把装有黑球和白球的两个盒子分开，并把其中一个带到很远的地方。虽然打开一个盒子，我们就会知道另一个盒子里球的颜色，但这并没有超光速的信息传递。

关于EPR佯谬，它作为一个量子效应和经典效应的主要区别，正体现在前文提到的Bell不等式上。同样考虑两个总自旋为0的电子（类似的系统可以由 $\eta$ 介子的衰变得到）。现在，我们对电子A测某一方向的自旋，对电子B测另一方向的自旋，两个方向可以不正交，那么两个测量结果在统计上会如何联系？

（以下出自Sakurai《Modern Quantum Mechanics》）如果我们有很多对纠缠中的电子，按照隐参量的理解，测量结果是由粒子的不知道但确定的属性决定的，三个方向自旋的测量结果可以分为8种：
$量子力学（科普部分）$
那么，比如，测量A在c方向的自旋得到+，B在a方向的自旋得到-的概率是：

$P(c+,a-)=\frac{N_1+N_3}{\sum N_i}$
同样，有：

$量子力学（科普部分）$
$P(b-,a-)=\frac{N_3+N_4}{\sum N_i}$

很显然， $量子力学（科普部分）$
这个长得有点像“三角形两边之和大于第三边”的不等式，就是贝尔不等式。然而，如果从量子力学出发进行推导，会发现，很容易举出反例使贝尔不等式不成立。比如，a沿x方向，b沿y方向，而c沿45度角的方向。于是，纠缠态中不正交的状态体现了一种经典统计无法理解的奇妙的相关性。
微观尺度上还有很多新奇的事情，比如粒子全同性。同类的微观粒子是完全相同、不可辨认的。两个电子是没有区别的，我们无法分辨它们。这个假设源于统计的结果。粒子是否具有全同性，会导致不同的统计分布。对于可分辨粒子，不同能级上的粒子数满足Boltzmann分布，但对于不可分辨粒子，则满足Fermi-Dirac分布或Bose-Einstein分布（取决于一个能级上是否只允许存在一个粒子），不同的统计分布在观测上有很大的区别，因此可以很容易被实验所区分。